Guide to Essential BioStatistics XII: Selecting a statistical test – choosing Nonparametric or Parametric Statistical Tests
In the previous articles in this series, we explored the Scientific Method and Proposing Hypotheses and Type-I and Type-II errors, Designing and implementing experiments (Significance, Power, Effect, Variance, Replication, Experimental Degrees of Freedom and Randomization), as well as Critically evaluating experimental data (Q-test; SD, SE, and 95%CI).
In the following articles, we will explore: Concluding whether to accept or reject the hypothesis (F- and T-tests, Chi-square, ANOVA and post-ANOVA testing).
In this twelfth article in the LabCoat Guide to BioStatistics series, we learn when to choose Nonparametric or Parametric Statistical Tests.
Inferential statistics
Inferential statistics enable us to test a hypothesis and draw conclusions, or inferences regarding a population through extrapolation from our experimental data sample.
Our choice of statistical method for hypothesis testing is based on whether the experimental data is normally distributed, and on the scale of the data.
Parametric and non-parametric tests
For normally distributed data, standard parametric tests such as the T-test and ANOVA tests are typically used, while nonparametric tests are appropriate if the data does not follow the normal distribution.
Parametric tests assume a Normal or Gaussian distribution of Measurement data at the Interval or Ratio scales (see previous article), while nonparametric do not – although they are subject to sample size requirements (see below). In addition to non-Gaussian Measurement data, Nonparametric tests are used for Categorical data at the Nominal or Ordinal scales.
Parametric tests are generally more powerful than non-parametric tests and are more likely to detect a significant effect when one indeed exists.
For this reason, many biologists tend to favor parametric tests rather than nonparametric tests, as any non-conformity to the prerequisites for parametric testing can often be circumvented through assumptions of normalcy, the identification and removal of outliers as well as data transformations.
In daily practice, it is thus usual for scientists to transform data from non-normal distributions, or to use parametric methods directly on datasets from non-normal distributions. With regard to the latter: if each treatment comprises less than 10 data values (due to practical or economic constraints), the consensus is that any test of normal distribution will be so compromised that neither data transformation nor the use of nonparametric tests will provide a significant benefit.
▶︎ A biological rule of thumb is that the small data sets commonly found in lab and greenhouse trials may be assumed to be normally distributed and analyzed using standard parametric tests.
NOTE: the information presented here comprises approximations and rules of thumb which are commonly used in designing and analyzing non-critical trials only. For critical experiments, nonparametric tests should be used if the data does not follow the normal distribution (before or after transformation) or sample size requirements for parametric tests – always seek the advice of a qualified statistician!
Overview of essential parametric and non-parametric methods
For hypothesis testing, specific parametric and nonparametric tests are available to evaluate different experimental datasets. Among these, the most commonly used include tests to compare a single group of data to a hypothetical value, to compare two paired or unpaired groups, or to compare three or more groups, as well as the prediction of values from previously measured values:
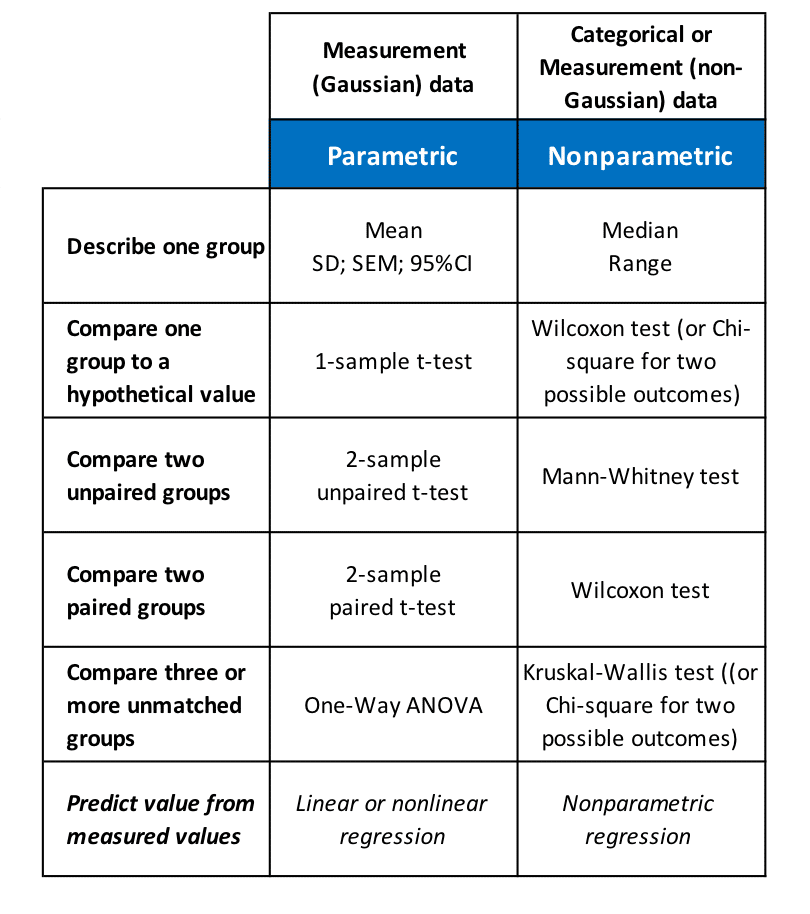
Figure 12.1: choosing statistical analysis methods.
We will obtain insight into the methods most commonly used in daily practice (t-tests, ANOVA and nonlinear regression for the estimation of ED50 values) in subsequent articles.
Microsoft Excel versus Statistics packages
This would be an excellent time to spend a minute or two considering software packages for statistical data analysis. Microsoft Excel is perhaps the most commonly used data software in biological research and is often used (and misused) for Statistical Data Analysis.
Excel is first and foremost a spreadsheet with added data analysis modules, and it is important to understand that the software has limitations relative to professional statistic packages. Excel is however excellent for data entry and data management and is accessible and sufficiently applicable for “quick-and-dirty” internal descriptive analyses and initial hypothesis testing carried out in research laboratories.
For more demanding applications (e.g., external reports and scientific papers) statisticians advise that Excel should only be used for data preparation, and this data should then be transferred to professional statistics packages for analysis. These results can then be reported directly or moved back to Excel for graphing and presentation purposes.
In Crop Protection Research, two of the most commonly used data packages for trial planning and statistical data analysis are the commercial ARM (Agricultural Research Manager) package, and the open-source statistical package, R.
Both have relatively steep learning curves, but once they have been mastered, they become indispensable. For researchers with limited scientific knowledge, the GraphPad suite of statistical packages provides real-time guidance during data analysis.
Thanks for reading – please feel free to read and share my other articles in this series!
The first two books in the LABCOAT GUIDE TO CROP PROTECTION series are now published and available in eBook and Print formats!
Aimed at students, professionals, and others wishing to understand basic aspects of Pesticide and Biopesticide Mode Of Action & Formulation and Strategic R&D Management, this series is an easily accessible introduction to essential principles of Crop Protection Development and Research Management.
A little about myself
I am a Plant Scientist with a background in Molecular Plant Biology and Crop Protection.
20 years ago, I worked at Copenhagen University and the University of Adelaide on plant responses to biotic and abiotic stress in crops.
At that time, biology-based crop protection strategies had not taken off commercially, so I transitioned to conventional (chemical) crop protection R&D at Cheminova, later FMC.
During this period, public opinion, as well as increasing regulatory requirements, gradually closed the door of opportunity for conventional crop protection strategies, while the biological crop protection technology I had contributed to earlier began to reach commercial viability.
I am available to provide independent Strategic R&D Management as well as Scientific Development and Regulatory support to AgChem & BioScience organizations developing science-based products.
For more information, visit BIOSCIENCE SOLUTIONS – Strategic R&D Management Consultancy.




